常见十大排序算法,动图演示(Python3实现)
小编在学习了数据结构、算法分析设计、Java、Python等之后,回顾所学发现见到最多的还是各种排序算法,站在前辈的肩膀上,决定做个总结。
一、概述:
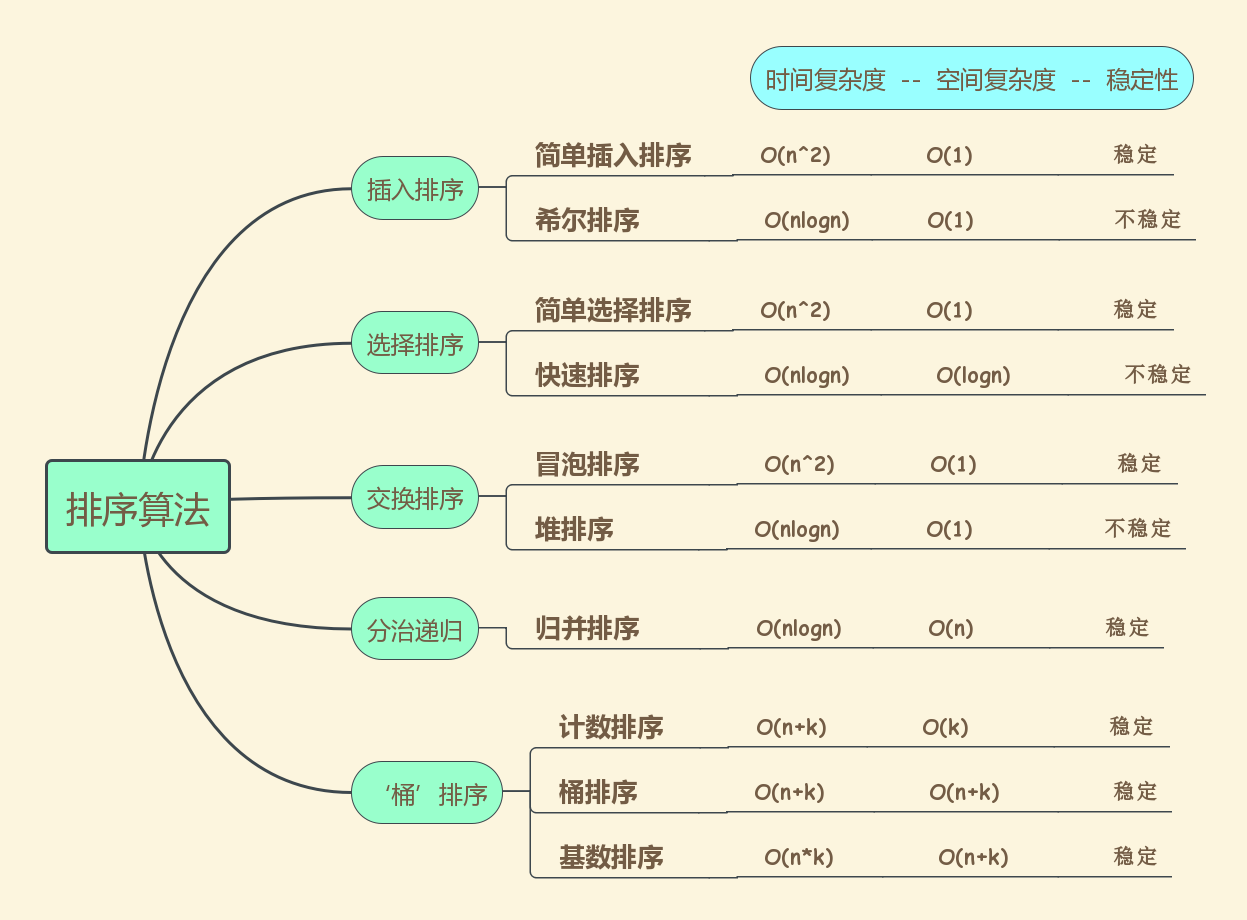
常见的排序算法基本可以分为十种(见下图),除此之外,还有结合多种算法思想基于他们的改进变种。
1. 插入排序、选择排序、交换排序:这三大类基于比较的排序算法,时间复杂度会随着优化程度在O(n^2)~O(nlogn)之间变化;
2. 希尔排序、快速排序、堆排序:它们分别代表着杰出的优化策略;
3. 归并排序:基于分治递归思想,将待排数据像二叉树一样分化至最简单的一个数排序问题,子问题合并时间复杂度可控制在O(n),不难想到整体时间复杂度取决于树的深度,即达到O(nlogn);
4. 计数排序、桶排序、基数排序:这三种线性时间排序算法本质上运用了相同的思想,先将数据按一定映射关系分组(桶),然后桶内排序,顺序输出。三种姑且称为‘桶’排序算法在分组函数使用上不同,导致分组粒度不同,带来的额外空间开销出现差异。这三种排序算法适用于数据满足一定的条件,否则额外的空间开销将无法承受。
二、算法简介及代码展示
1.简单插入排序
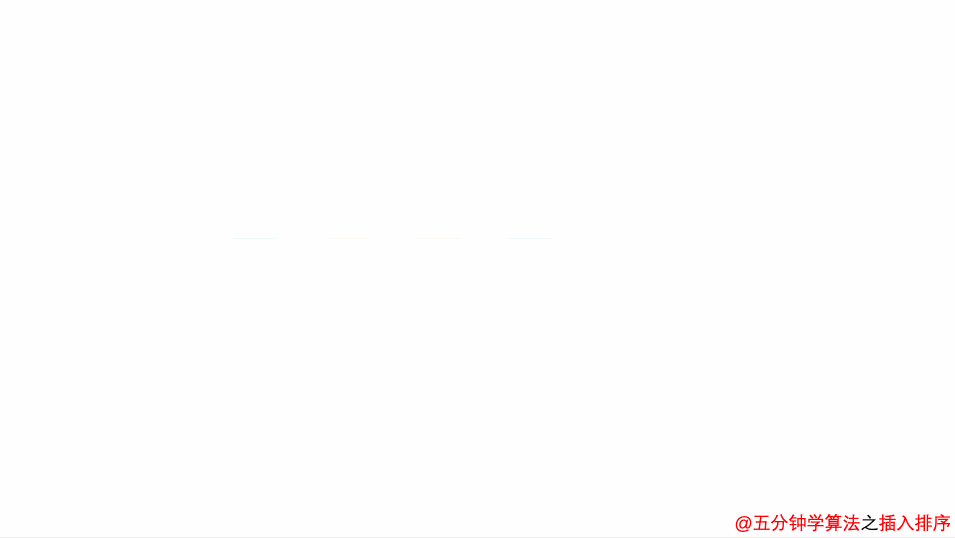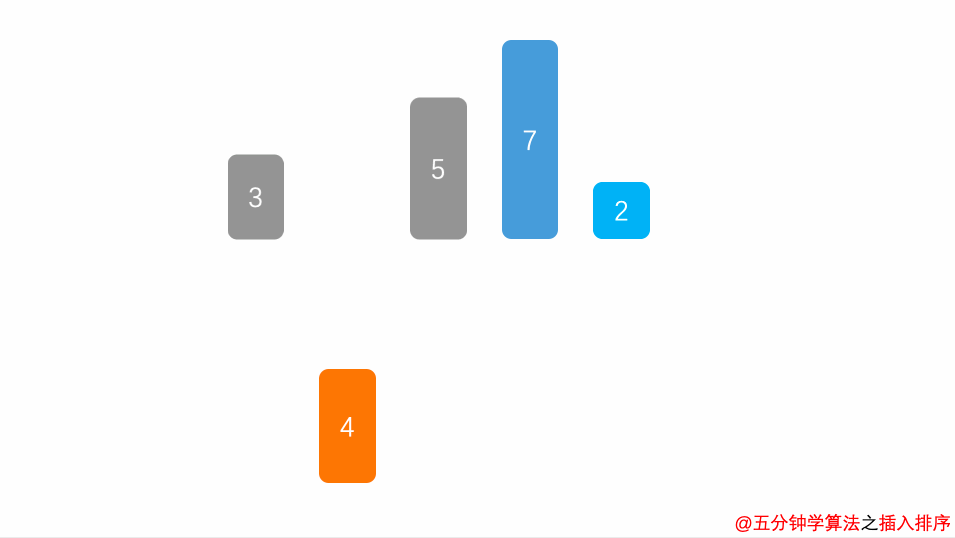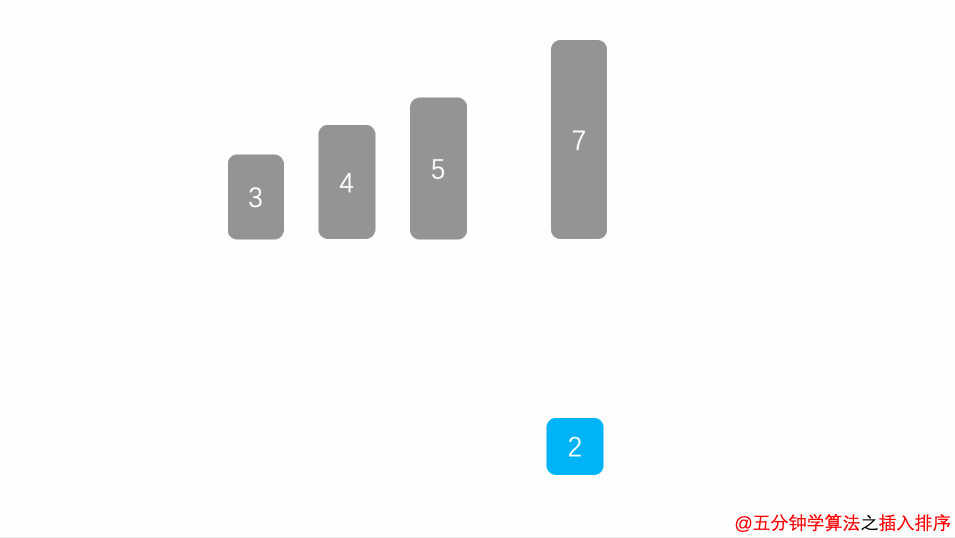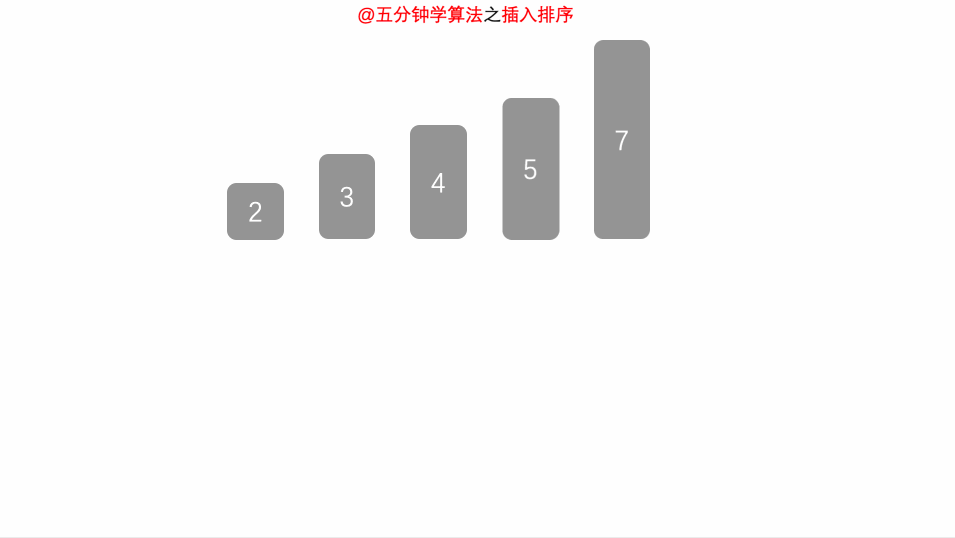
简单插入排序操作n-1轮,每轮将一个未排序树插入排好序列。
开始时默认第一个数有序,将剩余n-1个数逐个插入。插入操作具体包括:比较确定插入位置,数据移位腾出合适空位
代码如下:
def InsertSort(ls):
n=len(ls)
if n<=1:
return ls
for i in range(1,n):
j=i
target=ls[i] #每次循环的一个待插入的数
while j>0 and target<ls[j-1]: #比较、后移,给target腾位置
ls[j]=ls[j-1]
j=j-1
ls[j]=target #把target插到空位
return ls
2.希尔排序
希尔排序是插入排序的高效实现,对简单插入排序减少移动次数优化而来。
简单插入排序每次插入都要移动大量数据,前后插入时的许多移动都是重复操作,若一步到位移动效率会高很多。
若序列基本有序,简单插入排序不必做很多移动操作,效率很高。
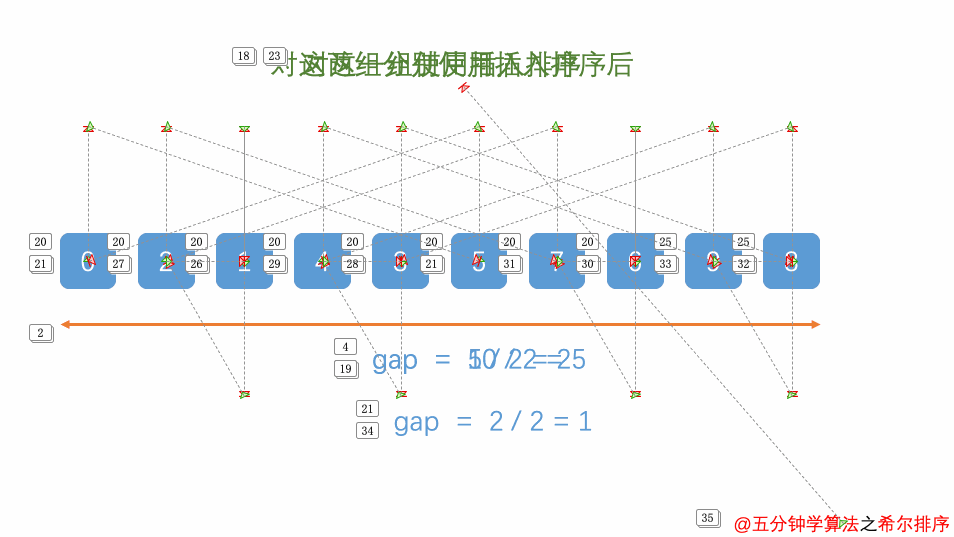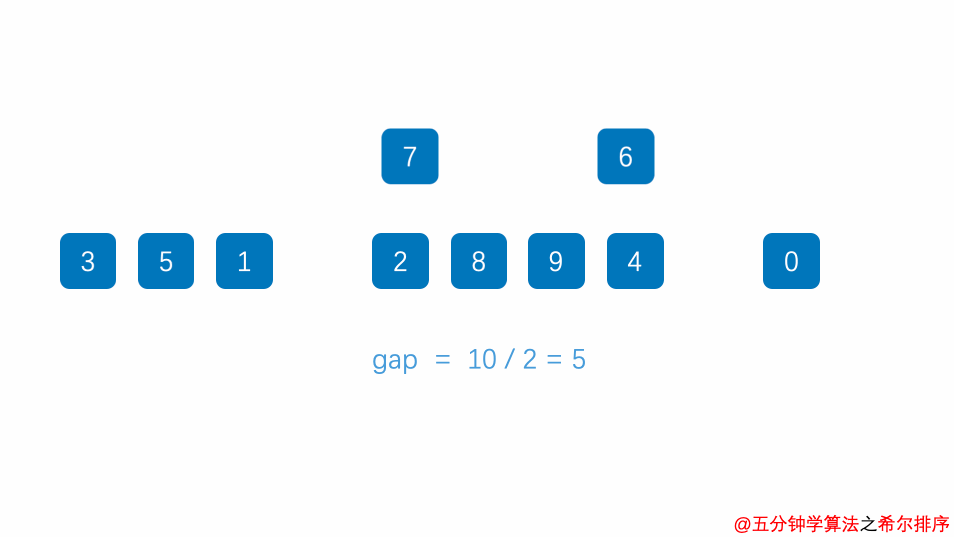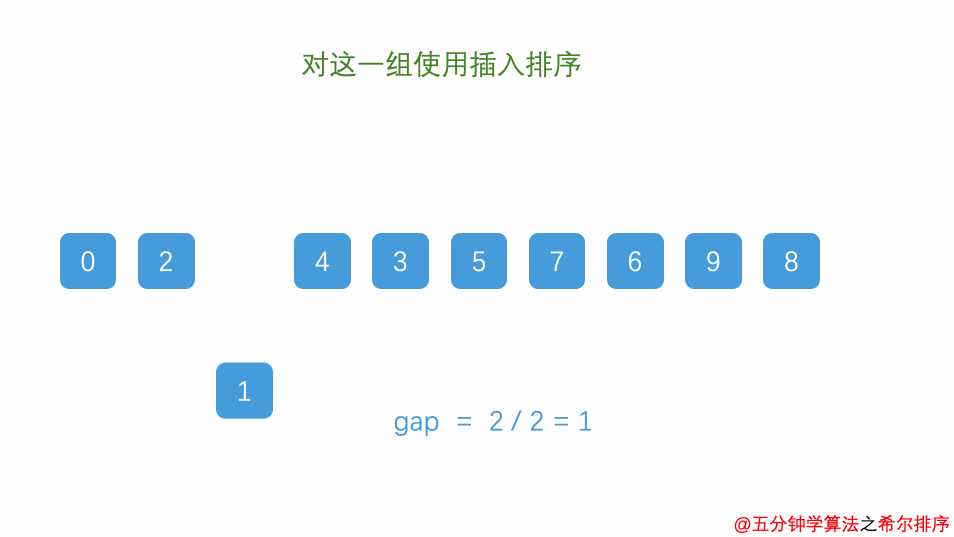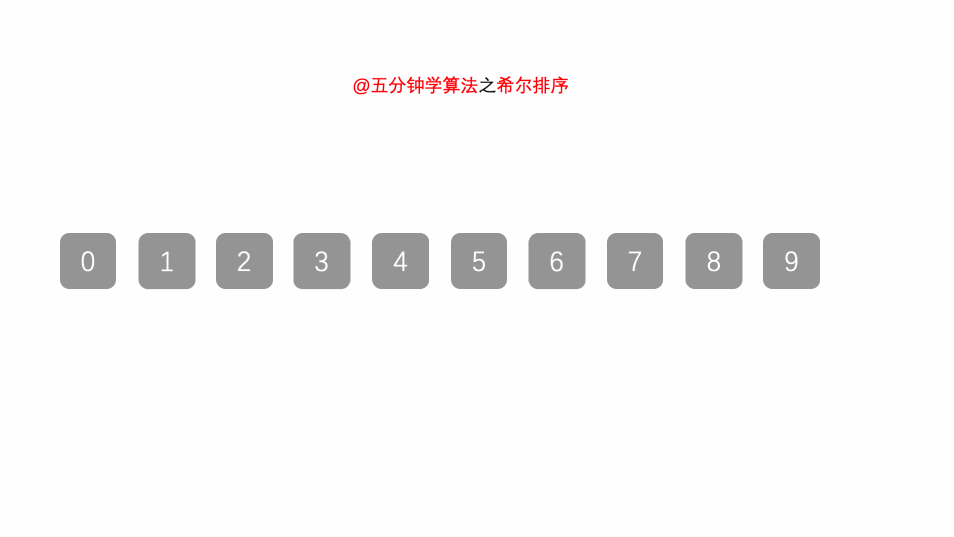
希尔排序将序列按固定间隔划分为多个子序列,在子序列中简单插入排序,先做远距离移动使序列基本有序;逐渐缩小间隔重复操作,最后间隔为1时即简单插入排序。
代码如下:
def ShellSort(ls):
def shellinsert(arr,d):
n=len(arr)
for i in range(d,n):
j=i-d
temp=arr[i] #记录要出入的数
while(j>=0 and arr[j]>temp): #从后向前,找打比其小的数的位置
arr[j+d]=arr[j] #向后挪动
j-=d
if j!=i-d:
arr[j+d]=temp
n=len(ls)
if n<=1:
return ls
d=n//2
while d>=1:
shellinsert(ls,d)
d=d//2
return ls
3.简单选择排序
选择排序同样对数据操作n-1轮,每轮找出一个最大(小)值。
操作指选择,即未排序数逐个比较交换,争夺最值位置,每轮将一个未排序位置上的数交换成已排序数,即每轮选一个最值。
代码如下:
def SelectSort(ls):
n=len(ls)
if n<=1:
return ls
for i in range(0,n-1):
minIndex=i
for j in range(i+1,n): #比较一遍,记录索引不交换
if ls[j]<ls[minIndex]:
minIndex=j
if minIndex!=i: #按索引交换
(ls[minIndex],ls[i])=(ls[i],ls[minIndex])
return ls
4.快速排序
快速排序基于选择划分,是简单选择排序的优化。
每次划分将数据选到基准值两边,循环对两边的数据进行划分,类似于二分法。
算法的整体性能取决于划分的平均程度,即基准值的选择,此处衍生出快速排序的许多优化方案,甚至可以划分为多块。

代码如下:
def QuickSort(ls):
def partition(arr,left,right):
key=left #划分参考数索引,默认为第一个数,可优化
while left<right:
while left<right and arr[right]>=arr[key]:
right-=1
while left<right and arr[left]<=arr[key]:
left+=1
(arr[left],arr[right])=(arr[right],arr[left])
(arr[left],arr[key])=(arr[key],arr[left])
return left
#递归调用
def quicksort(arr,left,right):
if left>=right:
return
mid=partition(arr,left,right)
quicksort(arr,left,mid-1)
quicksort(arr,mid+1,right)
#主函数
n=len(ls)
if n<=1:
return ls
quicksort(ls,0,n-1)
return ls
5.冒泡排序
冒泡排序对数据操作n-1轮,每轮找出一个最大(小)值。
操作指对相邻两个数比较与交换,每轮会将一个最值交换到数据列首(尾),像冒泡一样。
代码如下:
def BubbleSort(ls):
n=len(ls)
if n<=1:
return ls
for i in range (0,n):
for j in range(0,n-i-1):
if ls[j]>ls[j+1]:
(ls[j],ls[j+1])=(ls[j+1],ls[j])
return ls
6.堆排序
堆排序基于比较交换,是冒泡排序的优化。具体涉及大(小)顶堆的建立与调整。
大顶堆指任意一个父节点都不小于左右两个孩子节点的完全二叉树,根节点最大。
堆排序首先建立大顶堆(找出一个最大值),然后用最后一个叶子结点代替根节点后做大顶堆的调整(再找一个最大值),重复
以数组(列表)实现大顶堆时,从上到下,从左到右编号。父节点序号为n,则左右孩子节点序号分别为2*n+1、2*n+2
大顶堆的调整:将仅有根节点不满足条件的完全二叉树,调整为大顶堆的过程。
大顶堆调整方法:将根节点与较大一个儿子节点比较,不满足条件则交换。
若发生交换,将被交换儿子节点视作根节点重复上一步
大顶堆的建立:从最后一个非叶子节点开始到根节点结束的一系列大顶堆调整过程。

代码如下:
def HeapSort(ls):
def heapadjust(arr,start,end): #将以start为根节点的堆调整为大顶堆
temp=arr[start]
son=2*start+1
while son<=end:
if son<end and arr[son]<arr[son+1]: #找出左右孩子节点较大的
son+=1
if temp>=arr[son]: #判断是否为大顶堆
break
arr[start]=arr[son] #子节点上移
start=son #继续向下比较
son=2*son+1
arr[start]=temp #将原堆顶插入正确位置
#######
n=len(ls)
if n<=1:
return ls
#建立大顶堆
root=n//2-1 #最后一个非叶节点(完全二叉树中)
while(root>=0):
heapadjust(ls,root,n-1)
root-=1
#掐掉堆顶后调整堆
i=n-1
while(i>=0):
(ls[0],ls[i])=(ls[i],ls[0]) #将大顶堆堆顶数放到最后
heapadjust(ls,0,i-1) #调整剩余数组成的堆
i-=1
return ls
7.归并排序
希尔排序是插入排序的高效实现,对简单插入排序减少移动次数优化而来。
简单插入排序每次插入都要移动大量数据,前后插入时的许多移动都是重复操作,若一步到位移动效率会高很多。
若序列基本有序,简单插入排序不必做很多移动操作,效率很高。
希尔排序将序列按固定间隔划分为多个子序列,在子序列中简单插入排序,先做远距离移动使序列基本有序;逐渐缩小间隔重复操作,最后间隔为1时即简单插入排序。

代码如下:
def MergeSort(ls):
#合并左右子序列函数
def merge(arr,left,mid,right):
temp=[] #中间数组
i=left #左段子序列起始
j=mid+1 #右段子序列起始
while i<=mid and j<=right:
if arr[i]<=arr[j]:
temp.append(arr[i])
i+=1
else:
temp.append(arr[j])
j+=1
while i<=mid:
temp.append(arr[i])
i+=1
while j<=right:
temp.append(arr[j])
j+=1
for i in range(left,right+1): # !注意这里,不能直接arr=temp,他俩大小都不一定一样
arr[i]=temp[i-left]
#递归调用归并排序
def mSort(arr,left,right):
if left>=right:
return
mid=(left+right)//2
mSort(arr,left,mid)
mSort(arr,mid+1,right)
merge(arr,left,mid,right)
n=len(ls)
if n<=1:
return ls
mSort(ls,0,n-1)
return ls
8.计数排序
计数排序用待排序的数值作为计数数组(列表)的下标,统计每个数值的个数,然后依次输出即可。
计数数组的大小取决于待排数据取值范围,所以对数据有一定要求,否则空间开销无法承受。

代码如下:
def CountSort(ls):
n=len(ls)
num=max(ls)
count=[0]*(num+1)
for i in range(0,n):
count[ls[i]]+=1
arr=[]
for i in range(0,num+1):
for j in range(0,count[i]):
arr.append(i)
return arr
9.桶排序
桶排序实际上是计数排序的推广,但实现上要复杂许多。
桶排序先用一定的函数关系将数据划分到不同有序的区域(桶)内,然后子数据分别在桶内排序,之后顺次输出。
当每一个不同数据分配一个桶时,也就相当于计数排序。

代码如下:
def BucketSort(ls):
##############桶内使用快速排序
def QuickSort(ls):
def partition(arr,left,right):
key=left #划分参考数索引,默认为第一个数,可优化
while left<right:
while left<right and arr[right]>=arr[key]:
right-=1
while left<right and arr[left]<=arr[key]:
left+=1
(arr[left],arr[right])=(arr[right],arr[left])
(arr[left],arr[key])=(arr[key],arr[left])
return left
#递归调用
def quicksort(arr,left,right):
if left>=right:
return
mid=partition(arr,left,right)
quicksort(arr,left,mid-1)
quicksort(arr,mid+1,right)
#主函数
n=len(ls)
if n<=1:
return ls
quicksort(ls,0,n-1)
return ls
######################
n=len(ls)
big=max(ls)
num=big//10+1
bucket=[]
buckets=[[] for i in range(0,num)]
for i in ls:
buckets[i//10].append(i) #划分桶
for i in buckets: #桶内排序
bucket=QuickSort(i)
arr=[]
for i in buckets:
if isinstance(i, list):
for j in i:
arr.append(j)
else:
arr.append(i)
for i in range(0,n):
ls[i]=arr[i]
return ls
10.基数排序
基数排序进行多轮按位比较排序,轮次取决于最大数据值的位数。
先按照个位比较排序,然后十位百位以此类推,优先级由低到高,这样后面的移动就不会影响前面的。
基数排序按位比较排序实质上也是一种划分,一种另类的‘桶’罢了。比如,第一轮按各个位比较,按个位大小排序分别装入10个‘桶’中,‘桶’中个位相同的数据视作相等,桶是有序的,按序输出,后面轮次接力完成排序。

代码如下:
import math
def RadixSort(ls):
def getbit(x,i): #返回x的第i位(从右向左,个位为0)数值
y=x//pow(10,i)
z=y%10
return z
def CountSort(ls):
n=len(ls)
num=max(ls)
count=[0]*(num+1)
for i in range(0,n):
count[ls[i]]+=1
arr=[]
for i in range(0,num+1):
for j in range(0,count[i]):
arr.append(i)
return arr
Max=max(ls)
for k in range(0,int(math.log10(Max))+1): #对k位数排k次,每次按某一位来排
arr=[[] for i in range(0,10)]
for i in ls: #将ls(待排数列)中每个数按某一位分类(0-9共10类)存到arr[][]二维数组(列表)中
arr[getbit(i,k)].append(i)
for i in range(0,10): #对arr[]中每一类(一个列表) 按计数排序排好
if len(arr[i])>0:
arr[i]=CountSort(arr[i])
j=9
n=len(ls)
for i in range(0,n): #顺序输出arr[][]中数到ls中,即按第k位排好
while len(arr[j])==0:
j-=1
else:
ls[n-1-i]=arr[j].pop()
return ls
调试代码
# 此处调用上面的算法,以冒泡算法为例
arr = [int(x) for x in input("请输入待排序数列:\n").split()]
arr = BubbleSort(arr)
print("数列按序排列如下:")
for i in arr:
print(i,end=' ')
1. 十个排序算法都用函数封装,函数输入整数列表,返回整数列表;
2. 测试时输入以空格间隔的整数数列,split处理input采集的字符串,再经数据类型转换后变为整数列表后调用函数;
输出时采用循环逐个输出。
参照:https://www.cnblogs.com/yymor/p/10253527.html
来源:https://blog.csdn.net/weixin_44259720/article/details/103385439
本站大部分文章、数据、图片均来自互联网,一切版权均归源网站或源作者所有。
如果侵犯了您的权益请来信告知我们删除。邮箱:1451803763@qq.com



